AI_Learning/大模型架构/Transformer/2. 自注意力机制的计算.ipynb

{
 "cells": [
  {
   "cell_type": "markdown",
   "id": "87600e82-7e7c-4ca8-b1c3-08c4a28f8015",
   "metadata": {},
   "source": [
    "## 1. Transformer中的自注意力机制运算流程"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "5c1e9ba2-2afd-45a2-ad35-f04b1b49ccfd",
   "metadata": {},
   "source": [
    "现在我们知道注意力机制是如何运行的了，在Transformer当中我们具体是如何使用自注意力机制为样本增加权重的呢？来看下面的流程。\n",
    "\n",
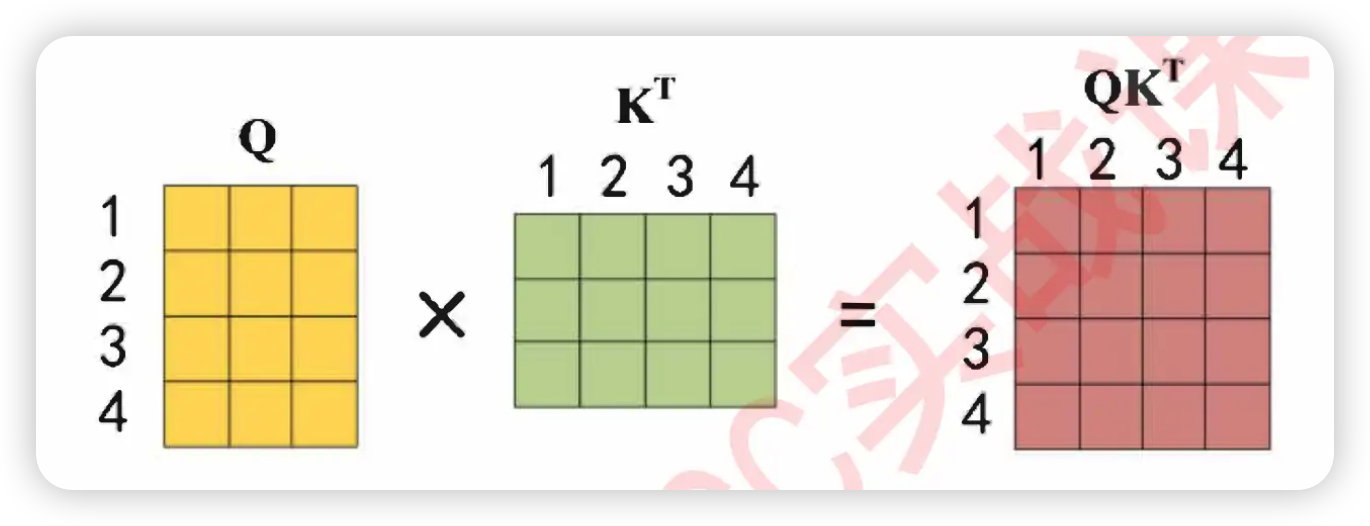
    "**Step1：通过词向量得到QK矩阵**\n",
    "\n",
    "首先，transformer当中计算的相关性被称之为是**注意力分数**，该注意力分数是在原始的注意力机制上修改后而获得的全新计算方式，其具体计算公式如下——\n",
    "\n",
    "  $$Attention(Q,K,V) = softmax(\\frac{QK^{T}}{\\sqrt{d_k}})V$$"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "89c841d9-3897-4777-aeb4-9ab47916ccd4",
   "metadata": {},
   "source": [
    "$QK^{T}$的过程中，点积是相乘后相加的计算流程，因此词向量的维度越高、点积中相加的项也就会越多，因此点积就会越大。此时，词向量的维度对于相关性分数是有影响的，在两个序列的实际相关程度一致的情况下，词向量的特征维度高更可能诞生巨大的相关性分数，因此对相关性分数需要进行标准化。在这里，Transformer为相关性矩阵设置了除以$\\sqrt{d_k}$的标准化流程，$d_k$就是特征的维度，以上面的假设为例，$d_k$=6。"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "1dfcddac-72dc-4276-b7b2-b6e3bd23e9ab",
   "metadata": {},
   "source": [
    "![](https://skojiangdoc.oss-cn-beijing.aliyuncs.com/2023DL/Live/NLP%26LLMs/2-3.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "284f963d-7b8b-4e27-b626-226d5e1ecc08",
   "metadata": {},
   "source": [
    "**Step3：softmax函数归一化**\n",
    "\n",
    "将每个单词之间的相关性向量转换成[0,1]之间的概率分布。例如，对AB两个样本我们会求解出AA、AB、BB、BA四个相关性，经过softmax函数的转化，可以让AA+AB的总和为1，可以让BB+BA的总和为1。这个操作可以令一个样本的相关性总和为1，从而将相关性分数转化成性质上更接近“权重”的[0,1]之间的比例。这样做也可以控制相关性分数整体的大小，避免产生数字过大的问题。\n",
    "\n",
    "经过softmax归一化之后的分数，就是注意力机制求解出的**权重**。"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "35212bed-7e01-4f14-a246-24742a04ccd0",
   "metadata": {},
   "source": [
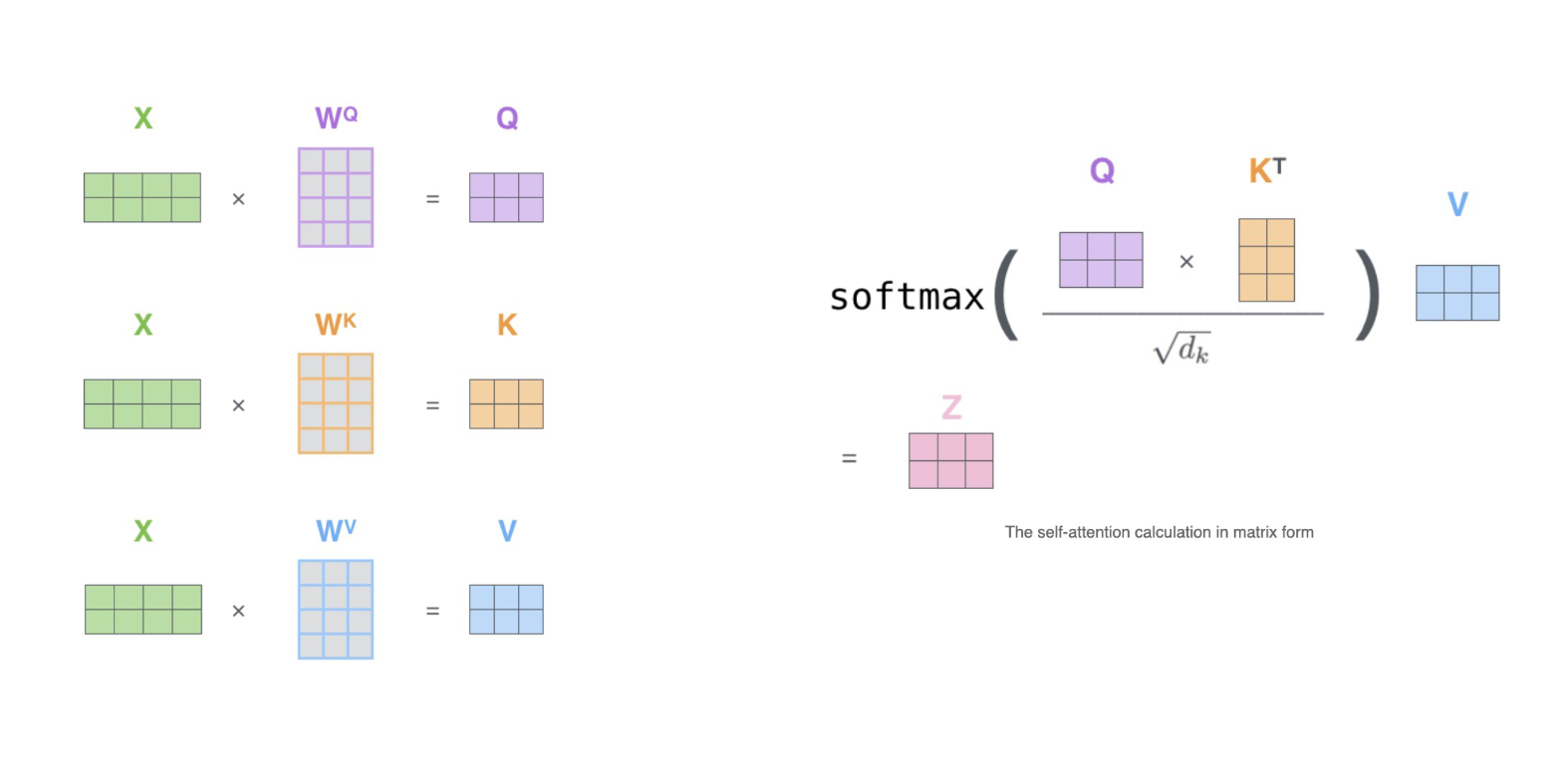
    "**Step4：对样本进行加权求和，建立样本与样本之间的关系**"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "dd256705-d8d4-48d3-83d4-49adfc29c589",
   "metadata": {},
   "source": [
    "![](https://skojiangdoc.oss-cn-beijing.aliyuncs.com/2023DL/transformer/image-11.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "5e9d7f3d-0b57-4272-ae76-1ae8dec4b128",
   "metadata": {},
   "source": [
    "现在我们已经获得了softmax之后的分数矩阵，同时我们还有代表原始特征矩阵值的V矩阵——"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "f3ab33c5-1f21-4765-a27d-23727c725b5a",
   "metadata": {},
   "source": [
    "$$\n",
    "\\mathbf{r} = \\begin{pmatrix}\n",
    "a_{11} & a_{12} \\\\\n",
    "a_{21} & a_{22}\n",
    "\\end{pmatrix},\n",
    "\\quad\n",
    "\\mathbf{V} = \\begin{pmatrix}\n",
    "v_{11} & v_{12} & v_{13} \\\\\n",
    "v_{21} & v_{22} & v_{23}\n",
    "\\end{pmatrix}\n",
    "$$\n",
    "二者相乘的结果如下："
   ]
  },
  {
   "cell_type": "markdown",
   "id": "b55e2403-0bbd-44c4-a050-f0c90b308af2",
   "metadata": {},
   "source": [
    "$$\n",
    "\\mathbf{Z(Attention)} = \\begin{pmatrix}\n",
    "a_{11} & a_{12} \\\\\n",
    "a_{21} & a_{22}\n",
    "\\end{pmatrix}\n",
    "\\begin{pmatrix}\n",
    "v_{11} & v_{12} & v_{13} \\\\\n",
    "v_{21} & v_{22} & v_{23}\n",
    "\\end{pmatrix}\n",
    "= \\begin{pmatrix}\n",
    "(a_{11}v_{11} + a_{12}v_{21}) & (a_{11}v_{12} + a_{12}v_{22}) & (a_{11}v_{13} + a_{12}v_{23}) \\\\\n",
    "(a_{21}v_{11} + a_{22}v_{21}) & (a_{21}v_{12} + a_{22}v_{22}) & (a_{21}v_{13} + a_{22}v_{23})\n",
    "\\end{pmatrix}\n",
    "$$"
   ]
  },
  {
   "cell_type": "markdown",
   "id": "ed14723a-80cf-4122-bd2f-be2fdde9a6bc",
   "metadata": {},
   "source": [
    "观察最终得出的结果，式子$a_{11}v_{11} + a_{12}v_{21}$不正是$v_{11}$和$v_{21}$的加权求和结果吗？$v_{11}$和$v_{21}$正对应着原始特征矩阵当中的第一个样本的第一个特征、以及第二个样本的第一个特征，这两个v之间加权求和所建立的关联，正是两个样本之间、两个时间步之间所建立的关联。\n",
    "\n",
    "在这个计算过程中，需要注意的是，列脚标与权重无关。因为整个注意力得分矩阵与特征数量并无关联，因此在乘以矩阵$v$的过程中，矩阵$r$其实并不关心一行上有多少个$v$，它只关心这是哪一行的v。因此我们可以把Attention写成：\n",
    "\n",
    "$$\n",
    "\\mathbf{Z(Attention)} = \\begin{pmatrix}\n",
    "a_{11} & a_{12} \\\\\n",
    "a_{21} & a_{22}\n",
    "\\end{pmatrix}\n",
    "\\begin{pmatrix}\n",
    "v_{11} & v_{12} & v_{13} \\\\\n",
    "v_{21} & v_{22} & v_{23}\n",
    "\\end{pmatrix}\n",
    "= \\begin{pmatrix}\n",
    "(a_{11}v_{1} + a_{12}v_{2}) & (a_{11}v_{1} + a_{12}v_{2}) & (a_{11}v_{1} + a_{12}v_{2}) \\\\\n",
    "(a_{21}v_{1} + a_{22}v_{2}) & (a_{21}v_{1} + a_{22}v_{2}) & (a_{21}v_{1} + a_{22}v_{2})\n",
    "\\end{pmatrix}\n",
    "$$\n",
    "\n",
    "很显然，对于矩阵$a$而言，原始数据有多少个特征并不重要，它始终都在建立样本1与样本2之间的联系。"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "id": "c5159295-643e-40e7-ada3-3d8c46437cd8",
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3 (ipykernel)",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.13.5"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 5
}